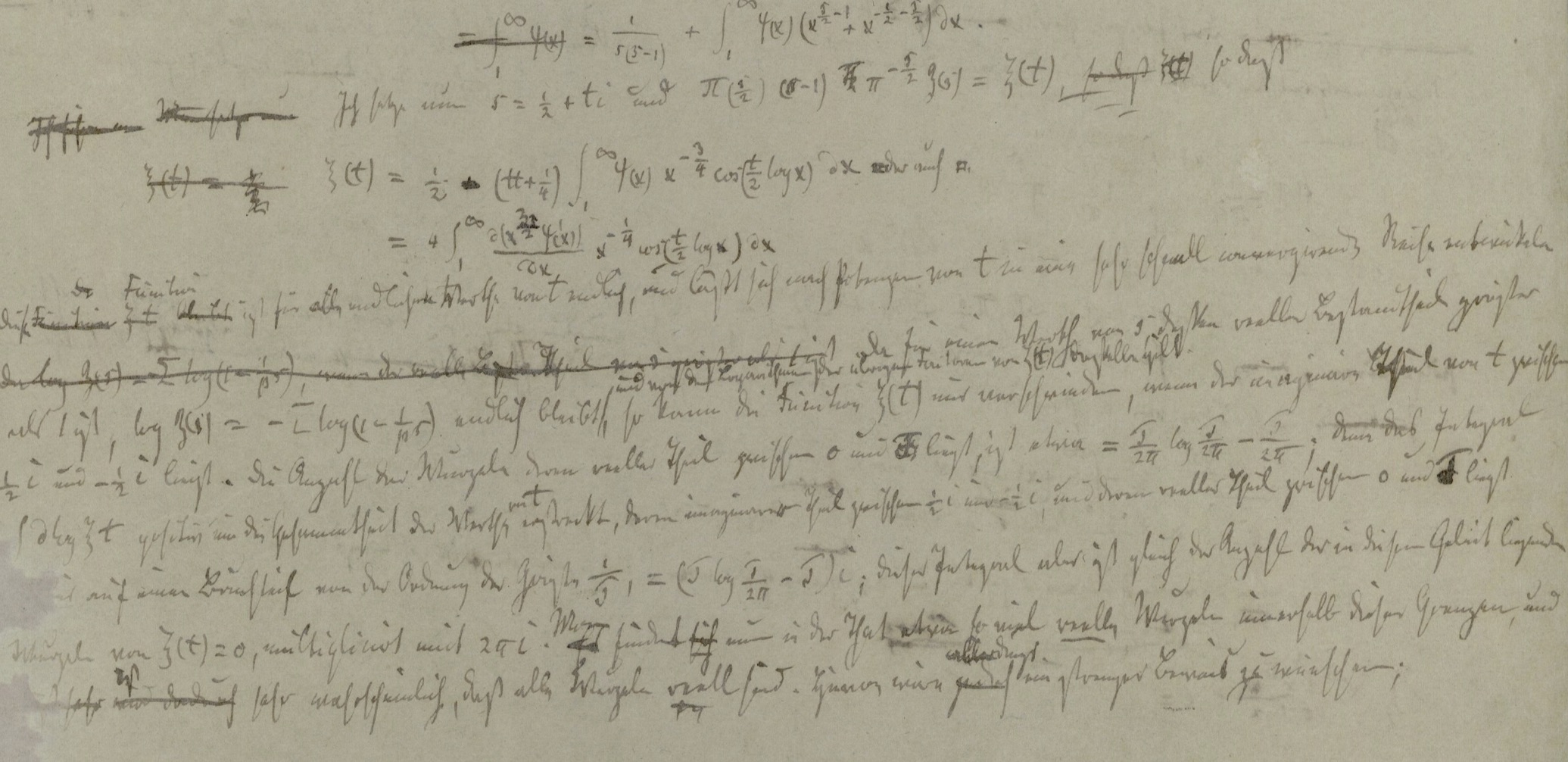
Bernhard Riemann német matematikus 1859-ben fogalmazta meg sejtését, amit sokan, így például maga Erdős Pál is az egész matematika legfontosabb problémájának tartott. Hogy pontosan mi is a Riemann-sejtés, abba most talán nem mennék bele. Akik tudják, tudják, akik nem tudják, azok valószínűleg pont ugyanannyit értenének belőle, mint én. A lényeg, hogy Riemann sejtése szerint saját Riemann-féle zéta-függvénye a prímszámok eloszlásáról is állíthat valamit. Ha sejtése igaznak bizonyul, akkor a prímszámok számának becslése pontosítható volna, aminek olyan gyakorlati területeken is komoly jelentősége van, mint például a kriptográfia.

Hogy a probléma nem triviális, azt mi sem bizonyítja jobban, hogy a sejtés megfogalmazása óta eltelt 159 évben még nem született széles körben elfogadott bizonyítás, bár időről időre vannak próbálkozások.

Most is akadt egy, amit ráadásul nem is egy tejfölös szájú zseni, hanem a matematika egyik nagy öregje, a már lovaggá is ütött, brit-libanoni Sir Michael Francis Atiyah, a 89 éves, visszavonult matematikus jelentett be a Heidelberg-díjasok fórumán, amikor felvázolt egy bizonyítást Riemann sejtésére.

Mivel a sejtés egyike az ún. millenniumi problémáknak, bizonyítását egymillió dollárral jutalmazzák.

A prímek - a csak saját magukkal vagy eggyel osztható, egynél nagyobb természetes számok - eloszlása ugyanis nem követ semmilyen rendezett mintát, így az eddig ismert prímszámokból nem következtethető ki a következő. Hiába tudjuk, hogy a 17, 19, 23 prímek, ebből nem következtethetünk arra, hogy a következő a 29 lesz, azután pedig a 31 következik. És bár a prímek a számsor elején még gyakran követik egymást, a számegyenesen tovább haladva egyre ritkábban, egyre nagyobb távolságra találni csak prímeket.

Riemann sejtése szerint zéta-fügvénye alkalmas lehet a prímszámok eloszlásának azonosítására. A gyakorlatban ez eddig az első tízezer milliárd prímszámra igaznak bizonyult, magát a sejtést ezzel még nem igazolták - mert mindig csak a prímszám ismeretében tudták ellenőrizni, hogy vajon igaz-e rá a sejtés.

"Senki sem hisz a Riemann-sejtés semmilyen bizonyításában, mert az annyira bonyolult. Senki sem bizonyította eddig, hát miért is bizonyítaná bárki most? Hacsak nem jut eszünkbe valami teljesen új" - mondta a Heidelberg-díjasok fórumán tartott hétfői előadásában Sir Michael, aki, mint azt sejthetik, pont egy ilyen teljesen új ötlettel állt elő. Bizonyításához a fizikából emelt át egy látszólag ide nem tartozó koncepciót, a finomszerkezeti állandót, amely az elektromágneses kölcsönhatás erősségét jellemzi.

Ezzel egyeseknek akadtak problémái, például azért, mert vannak arra utaló jelek, hogy a finomszerkezeti állandó valójában képes a változásra, amennyiben pedig nem állandó, akkor nem igazán alkalmas a Riemann-sejtés bizonyítására. Mivel Sir Michael Francis egyelőre csak egy ötoldalas összefoglalót (.pdf) közölt bizonyításáról, az azt megalapozó elméleti kutatásai pedig még publikációra várnak, egy darabig még izgulhatunk azon, hogy vajon sikerült-e végre bebizonyítani a sejtést. (Via Popsci)